Regelmäßiger Vieleckring berechnen
Rechner und Formeln für konzentrische Polygon-Ringe
Vieleckring Rechner
Regelmäßiger Vieleckring
Ein Vieleckring besteht aus zwei konzentrischen N-Ecken mit unterschiedlichen Seitenlängen. Ring-Geometrie mit variabler Dicke.
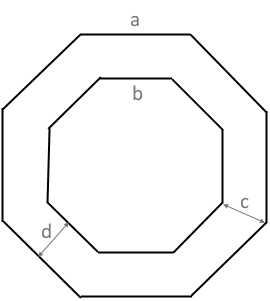
Vieleckring-Struktur
Das Diagramm zeigt einen Vieleckring mit äußerem und innerem Polygon.
Die Ringdicke variiert: an den Ecken (c) und an den Seiten (d).
Was ist ein regelmäßiger Vieleckring?
Ein regelmäßiger Vieleckring ist eine spezielle geometrische Struktur:
- Zwei konzentrische Polygone: Äußeres und inneres N-Eck
- Gleiche Eckenzahl: Beide Polygone haben n Ecken
- Gleiche Orientierung: Ecken sind radial ausgerichtet
- Variable Ringdicke: An Ecken (c) und Seiten (d) unterschiedlich
- Ring-Fläche: Differenz der beiden Polygon-Flächen
- Praktische Anwendung: Dichtungen, Flansche, Rohre
Konzentrische Polygon-Geometrie
Die konzentrische Anordnung zweier regelmäßiger Polygone erzeugt besondere Eigenschaften:
Zentrale Ausrichtung
- Gleicher Mittelpunkt für beide Polygone
- Identische Orientierung der Ecken
- Radiale Symmetrie-Achsen
- N-fache Rotationssymmetrie
Größenverhältnisse
- Äußere Seitenlänge: a > b (innere)
- Verhältnis bestimmt Ringdicke
- Skalierung aller Abmessungen
- Proportionale Flächendifferenz
Ringdicke-Analyse
Die Ringdicke variiert je nach Position am Polygon:
Ecken-Dicke (c)
- Radiale Dicke an den Polygon-Ecken
- Formel: c = (a-b)/(2·sin(π/n))
- Maximale Dicke des Rings
- Wichtig für Eck-Belastungen
Seiten-Dicke (d)
- Senkrechte Dicke an Seitenmitte
- Formel: d = (a-b)/(2·tan(π/n))
- Minimale Dicke des Rings
- Kritisch für Druckbelastung
Anwendungen von Vieleckringen
Vieleckringa finden in verschiedenen technischen Bereichen Anwendung:
Maschinenbau
- Dichtungsringe und O-Ringe
- Flanschverbindungen
- Lager und Kupplungen
- Zahnrad-Innenstrukturen
Bauwesen
- Polygonale Rohre und Kanäle
- Strukturelle Hohlprofile
- Architektonische Ringelemente
- Fenster- und Türrahmen
Verfahrenstechnik
- Reaktor-Innenauskleidungen
- Wärmetauscher-Strukturen
- Filter- und Siebsysteme
- Strömungs-Leitbleche
Design & Kunst
- Dekorative Rahmen und Ornamente
- Schmuck-Design (Ringe, Anhänger)
- Architektonische Verzierungen
- Kunst-Installationen
Formeln für den regelmäßigen Vieleckring
Ring-Fläche A
Differenz der beiden Polygon-Flächen
Gesamt-Umfang P
Summe beider Polygon-Umfänge
Ecken-Dicke c
Radiale Dicke an den Polygon-Ecken
Seiten-Dicke d
Senkrechte Dicke an den Seitenmitten
Äußerer Umkreisradius
Radius des äußeren Polygons
Innerer Umkreisradius
Radius des inneren Polygons
Dicken-Verhältnis
Verhältnis von Ecken- zu Seitendicke
Ring-Bedingung
Äußere Seite muss größer als innere sein
Rechenbeispiel für einen Vieleckring
Gegeben
Gesucht: Alle Eigenschaften des Oktagon-Rings
1. Ring-Grundmaße
Gesamtumfang und Ring-Fläche
2. Ringdicken berechnen
Ecken- und Seitendicke des Rings
3. Trigonometrische Werte für n=8
Alle Oktagon-Berechnungen basieren auf 22.5°-Winkeln
4. Vollständige Ring-Analyse
Der Oktagon-Ring zeigt typische Eigenschaften polygonaler Ringstrukturen
Der Vieleckring: Geometrie zwischen den Formen
Der regelmäßige Vieleckring ist eine faszinierende geometrische Struktur, die die Eigenschaften zweier konzentrischer Polygone miteinander verbindet. Diese scheinbar einfache Kombination erzeugt komplexe Beziehungen zwischen Flächen, Dicken und strukturellen Eigenschaften, die in Technik und Design vielfältige Anwendung finden.
Die Mathematik der Ringdicke
Das Faszinierendste am Vieleckring ist die variable Dicke:
- Eckendicke c > Seitendicke d: Der Ring ist an den Ecken immer dicker
- Verhältnis c/d = 1/cos(π/n): Abhängig nur von der Eckenzahl n
- Konvergenz zum Kreisring: Für n→∞ wird c = d (konstante Dicke)
- Extremfall Dreieck: n=3 zeigt maximalen Dickenunterschied
- Praktische Bedeutung: Wichtig für Belastungsanalysen und Materialverteilung
Konzentrische Geometrie und Symmetrie
Die konzentrische Anordnung erzeugt besondere Symmetrieeigenschaften:
Radiale Symmetrie
Der Ring besitzt n Symmetrieachsen durch die Ecken und n weitere durch die Seitenmitten. Jeder Sektor ist identisch.
Rotationssymmetrie
Drehung um 360°/n führt zur Selbstdeckung. Diese Eigenschaft ist wichtig für rotierende Maschinenteile.
Skalierungsverhalten
Alle Abmessungen skalieren proportional zu den Seitenlängen a und b. Das Verhältnis a:b bestimmt die relative Ringdicke.
Flächenbeziehungen
Die Ringfläche ist die Differenz zweier Polygon-Flächen. Sie skaliert quadratisch mit den Seitenlängen.
Ingenieurstechnische Anwendungen
Vieleckringa sind in der Technik weit verbreitet:
- Dichtungstechnik: Polygonale O-Ringe für spezielle Anwendungen
- Flanschverbindungen: Sechseck- oder Achteck-Flansche in der Rohrleitungstechnik
- Lager und Kupplungen: Polygonale Innenprofile für Formschluss
- Zahnradtechnik: Innenstrukturen von Hohlrädern
- Strukturbau: Hohlprofile mit polygonalen Querschnitten
- Verfahrenstechnik: Reaktor-Innenauskleidungen mit spezieller Geometrie
Berechnung und Optimierung
Die Berechnung von Vieleckringen erfordert besondere Aufmerksamkeit:
Strukturelle Analyse
Die variable Ringdicke führt zu ungleichmäßigen Spannungsverteilungen. Ecken sind oft kritische Bereiche für Spannungskonzentrationen.
Materialoptimierung
Die Kenntnis der Dickenverteilung ermöglicht optimierte Materialverteilung und Gewichtseinsparungen.
Fertigungsaspekte
Polygonale Ringe können oft einfacher gefertigt werden als Kreisringe, besonders bei Blechbearbeitung und Stanztechnik.
Toleranzen und Passungen
Die Berechnung exakter Abmessungen ist wichtig für Passungen und Montagetoleranzen in technischen Anwendungen.
Zusammenfassung
Der regelmäßige Vieleckring vereint die Eleganz geometrischer Symmetrie mit praktischer technischer Anwendbarkeit. Seine charakteristische variable Dicke - dicker an den Ecken, dünner an den Seiten - macht ihn zu einem interessanten Studienobjekt für Strukturmechanik und Materialoptimierung. Von der einfachen Formel zur Ringfläche bis zu komplexen Spannungsanalysen bietet der Vieleckring ein reiches Anwendungsfeld. In einer Welt, in der Leichtbau und Materialeffizienz immer wichtiger werden, zeigt der Vieleckring, wie geometrisches Verständnis zu praktischen Lösungen führen kann. Er steht als Beispiel für die tiefe Verbindung zwischen mathematischer Theorie und ingenieurstechnischer Praxis.
|
|