Regular Polygon Ring Calculator
Calculator and formulas for concentric polygon rings
Polygon Ring Calculator
Regular Polygon Ring
A polygon ring consists of two concentric N-gons with different side lengths. Ring geometry with variable thickness.
Polygon ring structure
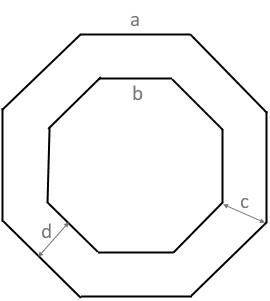
The diagram shows a polygon ring with outer and inner polygon.
The ring thickness varies: at corners (c) and at sides (d).
What is a regular polygon ring?
A regular polygon ring is a special geometric structure:
- Two concentric polygons: Outer and inner N-gon
- Same number of vertices: Both polygons have n vertices
- Same orientation: Vertices are radially aligned
- Variable ring thickness: Different at corners (c) and sides (d)
- Ring area: Difference of the two polygon areas
- Practical application: Seals, flanges, pipes
Concentric polygon geometry
The concentric arrangement of two regular polygons creates special properties:
Central alignment
- Same center point for both polygons
- Identical orientation of vertices
- Radial symmetry axes
- N-fold rotational symmetry
Size relationships
- Outer side length: a > b (inner)
- Ratio determines ring thickness
- Scaling of all dimensions
- Proportional area difference
Ring thickness analysis
The ring thickness varies depending on position on the polygon:
Corner thickness (c)
- Radial thickness at polygon corners
- Formula: c = (a-b)/(2·sin(π/n))
- Maximum thickness of the ring
- Important for corner loads
Side thickness (d)
- Perpendicular thickness at side center
- Formula: d = (a-b)/(2·tan(π/n))
- Minimum thickness of the ring
- Critical for pressure loading
Applications of polygon rings
Polygon rings find applications in various technical areas:
Mechanical engineering
- Sealing rings and O-rings
- Flange connections
- Bearings and couplings
- Gear internal structures
Construction
- Polygonal pipes and channels
- Structural hollow profiles
- Architectural ring elements
- Window and door frames
Process engineering
- Reactor internal linings
- Heat exchanger structures
- Filter and sieve systems
- Flow guide plates
Design & art
- Decorative frames and ornaments
- Jewelry design (rings, pendants)
- Architectural decorations
- Art installations
Formulas for the regular polygon ring
Ring area A
Difference of the two polygon areas
Total perimeter P
Sum of both polygon perimeters
Corner thickness c
Radial thickness at polygon corners
Side thickness d
Perpendicular thickness at side centers
Outer circumradius
Radius of the outer polygon
Inner circumradius
Radius of the inner polygon
Thickness ratio
Ratio of corner to side thickness
Ring condition
Outer side must be greater than inner
Calculation example for a polygon ring
Given
Find: All properties of the octagon ring
1. Ring basic measures
Total perimeter and ring area
2. Calculate ring thicknesses
Corner and side thickness of the ring
3. Trigonometric values for n=8
All octagon calculations are based on 22.5° angles
4. Complete ring analysis
The octagon ring shows typical properties of polygonal ring structures
The polygon ring: Geometry between forms
The regular polygon ring is a fascinating geometric structure that connects the properties of two concentric polygons. This seemingly simple combination creates complex relationships between areas, thicknesses, and structural properties that find diverse applications in engineering and design.
The mathematics of ring thickness
The most fascinating aspect of the polygon ring is its variable thickness:
- Corner thickness c > Side thickness d: The ring is always thicker at the corners
- Ratio c/d = 1/cos(π/n): Depends only on the number of vertices n
- Convergence to circular ring: For n→∞, c = d (constant thickness)
- Extreme case triangle: n=3 shows maximum thickness difference
- Practical significance: Important for stress analysis and material distribution
Concentric geometry and symmetry
The concentric arrangement creates special symmetry properties:
Radial symmetry
The ring has n symmetry axes through the vertices and n more through the side centers. Each sector is identical.
Rotational symmetry
Rotation by 360°/n results in self-congruence. This property is important for rotating machine parts.
Scaling behavior
All dimensions scale proportionally to the side lengths a and b. The ratio a:b determines the relative ring thickness.
Area relationships
The ring area is the difference of two polygon areas. It scales quadratically with the side lengths.
Engineering applications
Polygon rings are widely used in engineering:
- Sealing technology: Polygonal O-rings for special applications
- Flange connections: Hexagon or octagon flanges in piping technology
- Bearings and couplings: Polygonal internal profiles for form-fitting connections
- Gear technology: Internal structures of ring gears
- Structural engineering: Hollow profiles with polygonal cross-sections
- Process engineering: Reactor internal linings with special geometry
Calculation and optimization
The calculation of polygon rings requires special attention:
Structural analysis
The variable ring thickness leads to uneven stress distributions. Corners are often critical areas for stress concentrations.
Material optimization
Knowledge of thickness distribution enables optimized material distribution and weight savings.
Manufacturing aspects
Polygonal rings can often be manufactured more easily than circular rings, especially in sheet metal working and stamping technology.
Tolerances and fits
The calculation of exact dimensions is important for fits and assembly tolerances in technical applications.
Summary
The regular polygon ring combines the elegance of geometric symmetry with practical technical applicability. Its characteristic variable thickness - thicker at the corners, thinner at the sides - makes it an interesting study object for structural mechanics and material optimization. From the simple formula for ring area to complex stress analyses, the polygon ring offers a rich field of application. In a world where lightweight construction and material efficiency are becoming increasingly important, the polygon ring shows how geometric understanding can lead to practical solutions. It stands as an example of the deep connection between mathematical theory and engineering practice.
|
|