Hendecagon (11-gon) Calculator
Calculator and formulas for regular hendecagons
Hendecagon Calculator
Regular Hendecagon
A regular hendecagon has 11 equal sides and 11 equal interior angles (≈147.3°). The number 11 is a prime number.
Regular Hendecagon
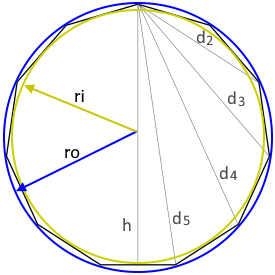
The diagram shows a regular hendecagon with all relevant parameters.
All 11 sides are equal in length, all interior angles measure ≈147.3°.
Properties of a regular hendecagon
A regular hendecagon (hendecagon) is a special geometric object:
- 11 equal sides: All side lengths are identical
- 11 equal angles: Each interior angle measures ≈147.273°
- Sum of angles: 9 × 180° = 1620°
- Prime number 11: Special mathematical properties
- Central angle: 360°/11 ≈ 32.727° per segment
- Construction: Complex geometric construction
The hendecagon and the prime number 11
The regular hendecagon is a prime number polygon with special properties:
Prime number properties
- 11 is indivisible (only by 1 and 11)
- No simple symmetry subdivisions
- Central angle is irrational (360°/11)
- Trigonometric values are algebraic
Mathematical challenge
- Complex construction with compass and straightedge
- Approximation methods often necessary
- Connection to number theory
- Cyclotomic polynomials of degree 11
Construction and mathematical properties
The regular hendecagon presents special constructive challenges:
Construction methods
- Constructible with compass and straightedge (Gauss)
- Requires solving a polynomial of degree 10
- Approximation constructions are more practical
- Central angle: 360°/11 ≈ 32.727°
Trigonometric values
- cos(π/11) and sin(π/11) are algebraic
- Exact values are very complex
- Numerical approximation is common
- Connection to Gaussian periods
Applications of the regular hendecagon
Regular hendecagons find special applications:
Numismatics & medals
- Special coins with hendecagon shape (rare)
- Collector medals and awards
- Historical tokens and jetons
- Artistic minting
Art & design
- Modern art objects and sculptures
- Graphic patterns and ornaments
- Architectural detail elements
- Symmetrical design studies
Science & mathematics
- Number theory and prime number research
- Constructive geometry studies
- Symmetry group investigations
- Algorithmic geometry
Engineering & technology
- Special gear configurations
- Rotationally symmetric components
- Sensor arrays with 11-fold symmetry
- Optical systems and apertures
Formulas for the regular hendecagon (hendecagon)
Area A
With tan(π/11) ≈ 0.2936
Perimeter P
Simple: 11 times the side length
Diagonal d₂
Shortest diagonal
Diagonal d₃
Middle short diagonal
Diagonal d₄
Middle long diagonal
Diagonal d₅ (longest)
Longest diagonal
Height h
With tan(π/22) ≈ 0.1409
Inner circle radius rᵢ
Apothem of the hendecagon
Circumcircle radius rₐ
With sin(π/11) ≈ 0.2817
Calculation example for a hendecagon
Given
Find: All properties of the regular hendecagon
1. Calculate basic measures
Perimeter and area
2. Calculate radii
Circumradius and inradius
3. All diagonals
All four different diagonal lengths
4. Complete summary
Complete characterization of the regular hendecagon
The regular hendecagon in mathematics and theory
The regular hendecagon occupies a special place among polygons, as it belongs to the class of prime number polygons. This property gives it unique mathematical characteristics and makes it an interesting object of study in constructive geometry and number theory.
Prime number properties and mathematical significance
The mathematical properties of the regular hendecagon are shaped by the prime number 11:
- Indivisibility: 11 is only divisible by 1 and itself
- Irrational angles: 360°/11 ≈ 32.727° is an irrational fraction of π
- Complex construction: Requires solving a polynomial of degree 10
- Gaussian theory: Constructible according to the Gauss-Wantzel theorem
- Cyclotomic polynomials: Connection to higher algebra
Constructive geometry and approximation methods
The construction of the regular hendecagon presents special challenges:
Exact construction
According to Gauss, the regular hendecagon is constructible with compass and straightedge, but this requires solving very complex algebraic equations.
Practical approximations
In practice, approximation methods are often used that provide sufficiently accurate results for technical applications.
Trigonometric values
The values of cos(π/11) and sin(π/11) are algebraic, but their exact form is extremely complex and unwieldy.
Numerical methods
Modern calculations use numerical approximations that are sufficiently precise for all practical purposes.
Applications and scientific relevance
Despite its constructive complexity, the hendecagon finds interesting applications:
- Number theory research: Study of prime number properties and cyclotomic fields
- Computer graphics: Algorithms for regular polygons with prime number sides
- Crystallography: Theoretical structures with 11-fold symmetry (quasicrystals)
- Optics: Special apertures and aperture designs with odd symmetry
- Mechanical engineering: Gears and rotating systems with prime number division
Modern computational aspects
In the digital age, the hendecagon gains new significance:
Algorithmic Geometry
Efficient algorithms for calculating and rendering prime number polygons in CAD systems and computer graphics.
Numerical Analysis
Development of precise numerical methods for approximating trigonometric functions of π/11.
Symmetry Studies
Investigation of symmetry groups and their applications in theoretical physics and materials science.
Computational Number Theory
Use in algorithms for prime number research and algebraic structure analysis.
Summary
The regular hendecagon stands as an example of the connection between pure mathematics and practical application. Its prime number properties make it a fascinating object of study for number theory and constructive geometry, while modern numerical methods enable its practical applicability in engineering and science. It shows how even seemingly "impractical" mathematical objects can gain new relevance in the digital world.
|
|