Decagon (10-gon) Calculator

Calculator and formulas for regular decagons

Decagon Calculator

Regular Decagon

A regular decagon has 10 equal sides and 10 equal interior angles (144°). It has close relations to the golden ratio.

Enter known parameter
Which parameter is known?
Value of the selected parameter
Calculation Results
Side length a:
Perimeter P:
Area A:
Height h:
Diagonal d5:
Diagonal d4:
Diagonal d3:
Diagonal d2:
Inner radius ri:
Outer radius ra:

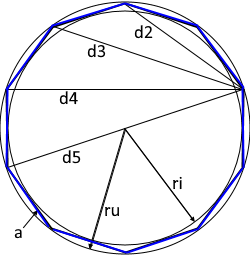
Regular Decagon

Decagon

The diagram shows a regular decagon with all relevant parameters.
All sides are equal, all interior angles are 144°.

Properties of a regular decagon

A regular decagon (10-gon) is a fascinating geometric object:

  • 10 equal sides: All side lengths are identical
  • 10 equal angles: Each interior angle is exactly 144°
  • Sum of angles: 8 × 180° = 1440°
  • Golden ratio: Close relation to φ = 1.618...
  • Symmetry: 10-fold rotational symmetry
  • Constructibility: Constructible with ruler and compass

The golden ratio in the decagon

The regular decagon exhibits a special relation to the golden ratio:

Golden ratio φ
\[\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.618\]

The golden ratio appears in many decagon formulas

Circumradius
\[r_a = \varphi \cdot a\]

The circumradius is φ times the side length

Construction and mathematical highlights

The regular decagon is a particularly interesting polygon:

Classical construction
  • Constructible with ruler and compass
  • Buildable using the golden ratio
  • Obtainable by bisecting a regular pentagon
  • Central angle: 360°/10 = 36°
Mathematical properties
  • Trigonometric values are algebraic
  • cos(36°) and sin(36°) have closed form expressions
  • Connections to Fibonacci numbers
  • Pentagonal symmetry as foundation

Applications of the regular decagon

Regular decagons appear in various fields:

Coins & Medals
  • Commemorative coins with decagon shapes
  • Medals and awards
  • Collector's editions
  • Historical coin shapes
Art & Design
  • Architectural floorplans
  • Rose windows in churches
  • Decorative ornaments
  • Modern design objects
Science & Technology
  • Crystallography and molecular structures
  • Antenna design for omnidirectional patterns
  • Optical systems
  • Rotationally symmetric components
Games & Entertainment
  • Board games with decagon tiles
  • Puzzles and placement games
  • Geometric riddles
  • Educational math media

Formulas for the regular decagon (10-gon)

Area A
\[A = \frac{5}{2} \sqrt{5 + 2\sqrt{5}} \cdot a^2 \approx 7.694 \cdot a^2\]

Complex formula with nested radicals

Perimeter P
\[P = 10 \cdot a\]

Simple: ten times the side length

Diagonal d₂
\[d_2 = \frac{1}{2}\sqrt{10 + 2\sqrt{5}} \cdot a \approx 1.902 \cdot a\]

Shortest diagonal

Diagonal d₃
\[d_3 = \frac{1}{2}\sqrt{14 + 6\sqrt{5}} \cdot a \approx 2.618 \cdot a\]

Middle diagonal

Diagonal d₄ (Height h)
\[d_4 = h = \sqrt{5 + 2\sqrt{5}} \cdot a \approx 3.078 \cdot a\]

Longest diagonal = height

Diagonal d₅
\[d_5 = (1 + \sqrt{5}) \cdot a \approx 3.236 \cdot a\]

Maximum diagonal tied to the golden ratio

Circumradius rₐ
\[r_a = \frac{1 + \sqrt{5}}{2} \cdot a \approx 1.618 \cdot a = \varphi \cdot a\]

Golden ratio times the side length

Inradius rᵢ
\[r_i = \frac{1}{2}\sqrt{5 + 2\sqrt{5}} \cdot a \approx 1.539 \cdot a\]

Radius of the inscribed circle

Example calculation for a decagon

Given
Side length a = 4

Find: All properties of the regular decagon

1. Basic measures
\[P = 10 \times 4 = 40\] \[A = 7.694 \times 16 = 123.11\]

Perimeter and area

2. Radii
\[r_a = 1.618 \times 4 = 6.47\] \[r_i = 1.539 \times 4 = 6.16\]

Circumradius and inradius

3. All diagonals
d₂ = 1.902 × 4 = 7.61 d₃ = 2.618 × 4 = 10.47
d₄ = h = 3.078 × 4 = 12.31 d₅ = 3.236 × 4 = 12.94

All four different diagonal lengths

4. Complete summary
Side length a = 4.00 Perimeter P = 40.00 Area A = 123.11 Height h = 12.31
Circumradius = 6.47 Inradius = 6.16 Interior angle = 144° Central angle = 36°

Complete characterization of the regular decagon

The regular decagon in mathematics and nature

The regular decagon holds a special place among the regular polygons. Its close relation to the golden ratio and the properties of the regular pentagon make it a mathematically fascinating object with many practical applications.

Mathematical depth and the golden ratio

The mathematical properties of the regular decagon reveal remarkable depth:

  • Golden ratio φ: Appears in nearly all key formulas (φ = (1+√5)/2 ≈ 1.618)
  • Algebraic roots: All trigonometric values have closed-form expressions
  • Constructibility: Constructible with ruler and compass (Gauss criterion satisfied)
  • Pentagonal symmetry: Based on the 5-fold rotational symmetry of the pentagon
  • Diophantine properties: Connections to number-theoretic problems

Construction and geometric elegance

Constructing the regular decagon reveals geometric elegance:

Classical methods

Construction via the golden ratio, by bisecting a regular pentagon or by dividing the circle into ten equal parts using the 36° angle.

Modern approaches

Coordinate geometry, trigonometric methods and algorithmic constructions in CAD systems use the algebraic properties.

Symmetry properties

10-fold rotational symmetry, 10 mirror axes and the relation to the dihedral group D₁₀ make it a perfect example of discrete symmetry.

Approximation properties

Excellent circle approximation while keeping formula and construction complexity manageable.

Conclusion

The regular decagon combines mathematical beauty with practical applicability. Its relation to the golden ratio, constructibility with classical tools and diverse applications make it a timeless geometric object. From pure mathematics to design and engineering, it demonstrates the elegance and universality of geometric principles.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?

More polygons

Triangle • Square • Pentagon • Hexagon • Heptagon • Octagon • Nonagon • Decagon • Hendecagon • Dodecagon • Hexadecagon • N-Gon • Polygon ring • Concave hexagon • Axial Symmetric Pentagon • Irregular, stretched Hexagon • Irregular, stretched Octagon • Pentagram • Hexagram • Octagram • Star of Lakshmi