Hexagon Calculator
Calculator and formulas for regular hexagons
Hexagon Calculator
Regular Hexagon
A regular hexagon has 6 equal sides and 6 equal angles (120°). It is nature's perfect form.
Regular Hexagon
The diagram shows a regular hexagon with all relevant parameters.
All 6 sides are equal, all interior angles are 120°.
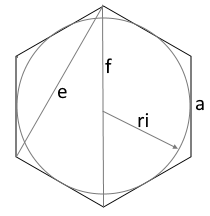
Properties of a regular hexagon
A regular hexagon is one of the most elegant geometric forms:
- 6 equal sides: All side lengths are identical
- 6 equal angles: Each interior angle is exactly 120°
- Angle sum: 4 × 180° = 720°
- Natural perfection: Most common form in nature
- Central angle: 360°/6 = 60° per segment
- Tessellation: Perfect tiling possible
The hexagon in nature
The regular hexagon is nature's preferred form:
Crystal structures
- Snowflakes show 6-fold symmetry
- Quartz and other minerals
- Ice crystal lattice (hexagonal)
- Graphite layer structure
Biological forms
- Honeycombs (perfect space utilization)
- Basalt columns (cooling of lava)
- Connection structures in organisms
- Cell structures and tissues
The honeycomb: Nature's perfection
The honeycomb is the perfect example of the hexagon's efficiency:
Mathematical perfection
- Maximum area with minimum perimeter
- Least material consumption (wax)
- Perfect tessellation without gaps
- Structural stability
The honeycomb theorem
- Mathematically proven optimality
- Isoperimetric problem solved
- Inspires architecture and technology
- Model for lightweight constructions
Applications of the regular hexagon
Regular hexagons find diverse practical applications:
Technology & engineering
- Hex bolts and nuts
- Tool handles (screwdrivers)
- Machine components
- Honeycomb sandwich construction
Architecture & design
- Tiles and floor coverings
- Facade design
- Structural lightweight elements
- Modern building geometry
Games & entertainment
- Board games with hexagonal fields
- Strategy games (Settlers of Catan)
- Video game maps (Civilization)
- Puzzles and tile games
Science & research
- Molecular chemistry (benzene ring)
- Materials science
- Nanotechnology (graphene)
- Optics and photonics
Formulas for the regular hexagon
Area A
With √3 ≈ 1.732 (particularly elegant)
Perimeter P
Simple: 6 times the side length
Short diagonal e
Corresponds to the height of the hexagon
Long diagonal f
Simple: twice the side length
Inradius rᵢ
Apothem of the hexagon
Circumradius rₐ
Circumradius = side length (unique!)
Side length from diagonals
Reverse calculations
Interior angle α
Each of the 6 interior angles
Calculation example for a hexagon
Given
Find: All properties of the regular hexagon
1. Calculate basic measures
Perimeter and area
2. Calculate radii
Circumradius and inradius
3. Calculate diagonals
The two different diagonal lengths
4. Special properties
The hexagon consists of 6 equilateral triangles!
The regular hexagon: Perfection in nature and technology
The regular hexagon is arguably the most elegant and practical of all geometric forms. It unites mathematical beauty with functional perfection and demonstrates like no other form the principle of efficiency in nature and technology.
Mathematical elegance and unique properties
The mathematical properties of the regular hexagon show remarkable elegance:
- Perfect symmetry: 6-fold rotational and mirror symmetry
- Unique radius property: Circumradius = side length (rₐ = a)
- √3 relationships: Many formulas contain √3 as an elegant factor
- 60° geometry: Central angle 60° leads to equilateral triangles
- Simple construction: Constructible with compass alone
- Perfect tessellation: Seamless tiling of the plane
The honeycomb as model of perfection
The most famous example of the hexagon's perfection is the honeycomb:
The honeycomb problem
For centuries, mathematics puzzled over why bees build hexagonal combs. In 1999, Thomas Hales proved the "Honeycomb Conjecture": The hexagon is the optimal form for space division.
Isoperimetric optimum
For a given perimeter, the hexagon has the largest area of all tessellating forms. This minimizes wax consumption while maximizing honey storage capacity.
Structural advantages
The 120° angles are optimal for force distribution. Each wall contributes equally to stability without material waste through over-dimensioning.
Natural laws in action
Bees don't "calculate" - they follow physical laws. Surface tension and energy minimization automatically lead to the hexagonal form.
Technical applications and modern innovation
The efficiency of the hexagon inspires modern technology and design:
- Lightweight construction revolution: Honeycomb sandwich construction in aerospace
- Materials science: Graphene and hexagonal carbon lattices
- Mechanics: Hex bolts for optimal force transmission
- Architecture: Structural efficiency in facades and load-bearing structures
- Game design: Hexagonal grids for strategic board games
- Nanotechnology: Molecular structures and self-organization
Hexagon geometry in various sciences
The hexagon permeates various scientific fields:
Chemistry and molecular structure
The benzene ring (C₆H₆) is the basic element of organic chemistry. Its hexagonal structure gives aromatic compounds special stability.
Physics and crystallography
Many crystal lattices are based on hexagonal symmetry. Graphite, ice, and numerous minerals show this preferred arrangement.
Biology and evolution
Not only bees - other organisms also use hexagonal structures for efficiency: turtle shells, bird eyes, plant tissue.
Geology and natural phenomena
Giant's Causeway, columnar basalt, and other geological formations arise through the natural tendency toward hexagonal structure.
Future perspectives and innovation
The hexagon continues to inspire modern innovation:
- Metamaterials: Hexagonal structures for new optical and acoustic properties
- 3D printing: Honeycomb infill for weight optimization with high strength
- Robotics: Hexapod robots use 6-fold symmetry for stability
- Solar energy: Hexagonal solar cells for optimal area utilization
- Urban planning: Hexagonal city planning for efficient traffic flow
Summary
The regular hexagon stands as a symbol for the perfect connection of mathematical elegance and practical efficiency. From the molecular level to architectural masterpieces, it shows how natural laws lead to optimal solutions. Its unique properties - particularly the relationship rₐ = a and perfect tessellation - make it the "perfect form". In a world striving for sustainability and efficiency, the hexagon remains a timeless model for design and innovation.
|
|