Calculate Irregular Hexagon
Calculator and formulas for the elongated hexagon
Irregular Hexagon Calculator
The irregular hexagon
An irregular hexagon is an elongated hexagon with two different side lengths but equal interior angles of 120°.
Hexagon structure
The irregular hexagon has two different side lengths.
All interior angles measure uniformly 120°.
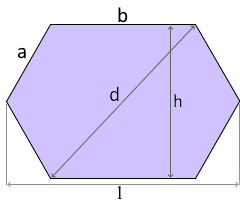
The irregular elongated hexagon
The irregular hexagon is a special form of the hexagon with unique properties:
- Six sides: 4 sides of length a, 2 sides of length b
- Equal angles: All interior angles measure 120°
- Elongated form: Rectangular center part with 60° chamfers
- Simple calculation: Only two parameters required
- √3 mathematics: Height h = a·√3 (60° trigonometry)
- Practical form: Frequently used in design and technology
120° angle properties
The angle structure of the irregular hexagon is based on 60° geometry:
Interior angles
- All 6 interior angles = 120°
- Sum: 6 × 120° = 720°
- Corresponds to the hexagon formula: (6-2) × 180°
- 30° more than a right angle
Exterior angles
- All 6 exterior angles = 60°
- Sum: 6 × 60° = 360°
- Corresponds to the general polygon rule
- Fundamental for equilateral triangles
√3 geometry and structure
The geometric structure of the elongated hexagon:
Construction principle
- Center part: Rectangle of size b × h
- Side parts: 2 parallelograms
- Corners: 4 equilateral triangles (60°)
- Symmetry: Horizontally symmetric
√3 mathematics
- Height: h = a·√3
- Length: l = a + b
- √3 ≈ 1.732: Fundamental for 60° geometry
- Elegant formulas: Simple relationships
Applications of the irregular hexagon
The elongated hexagon finds diverse practical applications:
Industry & technology
- Screw head profiles (elongated hex heads)
- Special tool forms
- Pipeline connection pieces
- Gear and machine components
Architecture & design
- Window and door forms
- Tile and flooring patterns
- Column and structural profiles
- Decorative wall elements
Design & art
- Logo design and corporate identity
- Furniture design and table forms
- Jewelry and decorative objects
- Textile patterns and ornaments
Nature & biology
- Crystal structures and minerals
- Honeycomb-like structures
- Molecular geometry
- Biological cell structures
Formulas for the irregular hexagon
Length l
Simple addition of the two side lengths
Height h
Height based on 60° trigonometry
Perimeter P
4 short sides plus 2 long sides
Diagonal d
Pythagorean theorem applied to height and long side
Area A
Hexagon portion plus rectangle extension
√3 constant
Fundamental for 60° angle geometry
Interior angles
All interior angles are equal
Calculation example for an irregular hexagon
Given
Find: All geometric properties of the elongated hexagon
1. Calculate basic dimensions
Height with √3 and simple length sum
2. Perimeter and diagonal
Total perimeter and main diagonal
3. Area calculation
Composition of hexagon portion and rectangle extension
4. Complete irregular hexagon
The complete elongated hexagon - elegant √3 mathematics meets practical design
The irregular hexagon: √3 geometry meets design
The irregular elongated hexagon is an elegant example of how the natural √3 geometry of 60° angles can be combined with practical design requirements. As a hexagon with two different side lengths but uniform 120° interior angles, it connects the harmony of honeycomb structures with the flexibility of functional design, finding broad application from industry to art.
The magic of √3 geometry
The specialty of the elongated hexagon lies in its √3-based mathematics:
- 120° interior angles: Perfect 60° exterior angles create equilateral triangles
- √3 height: h = a·√3 ≈ 1.732·a from 60° trigonometry
- Natural proportions: Corresponds to crystal structure of many minerals
- Simple formulas: Despite √3, mathematically very manageable
- Modular expandable: Rectangle extension through parameter b
- Honeycomb relationship: Basic geometry of nature's most efficient structures
120° - The perfect compromise
The uniform interior angle of 120° makes this hexagon particularly valuable:
Natural harmony
120° is the interior angle of a regular hexagon - the same geometry that gives honeycombs their optimal space division.
Crystallography
Many crystal structures are based on 120° angles, from quartz to snowflakes - a fundamental order of nature.
Technical advantages
120° angles are mechanically stable and enable uniform force distribution - ideal for construction applications.
Aesthetic effect
The combination of sharp 120° angles and flowing transitions creates a balanced visual tension.
Versatile application fields
The elongated hexagon finds application in surprisingly many areas:
- Screw technology: Elongated hex head screws for special applications
- Architecture: Window forms and structural profiles
- Furniture design: Tables and work surfaces with functional elegance
- Tile technology: Parquet and flooring patterns
- Crystal growth: Growth forms for synthetic crystals
- Optics: Lens and prism geometry for special applications
Learning from nature: Biomimetics
The elongated hexagon shows how biomimetics works:
Honeycomb principle
The hexagonal basic structure maximizes volume with minimal material consumption - an optimization principle of evolution.
Crystalline order
The 120° angles correspond to energetically favorable arrangements in matter - from atoms to galaxies.
Technical implementation
Modern materials like honeycomb structures and metamaterials use this geometry for lightweight and strength.
Design innovation
From Tesla battery cells to smartphone displays - hexagonal geometry optimizes functionality and aesthetics equally.
Summary
The irregular elongated hexagon unites nature's wisdom with the requirements of modern technology and design. Its √3-based mathematics reflects the fundamental ordering principles of the universe, while its practical applicability ranges from screw heads to crystal structures. The uniform 120° angles create structural stability and aesthetic harmony, while the variable extension enables functional flexibility. In a world seeking both efficiency and beauty, the elongated hexagon shows that the best solutions are often the simplest - mathematically elegant, technically practicable, and visually appealing. It reminds us that true innovation lies not in overcoming nature, but in intelligently adapting its timeless principles and making them usable for human needs.
|
|