Regular N-gon Calculator
Universal calculator for all regular polygons
N-gon Calculator
Universal Polygon Calculator
A regular N-gon has N equal sides and N equal angles. Universal formulas for all polygons.
Regular N-gon
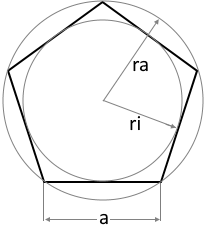
The diagram shows an example polygon with inscribed and circumscribed circles.
All N sides are equal in length, all interior angles are equal.
The universal N-gon calculator
A regular N-gon is the most general form of a regular polygon:
- N equal sides: All side lengths are identical
- N equal angles: Each interior angle = 180°(N-2)/N
- Sum of angles: (N-2) × 180°
- Central angle: 360°/N per segment
- N-fold symmetry: Rotational and reflection symmetry
- Universal formulas: Work for all N ≥ 3
Universal polygon formulas
These universal formulas work for all regular polygons:
Basic formulas
- Perimeter: P = N · a
- Area: A = (N/4) · cot(π/N) · a²
- Interior angle: α = 180°(N-2)/N
- Central angle: β = 360°/N
Circle relationships
- Circumradius: rₐ = a/(2·sin(π/N))
- Inradius: rᵢ = a/(2·tan(π/N))
- Ratio: rₐ/rᵢ = 1/cos(π/N)
- Apothem = Inradius
Known polygon examples
Overview of the most common regular polygons and their properties:
Basic polygons
- N=3: Triangle (60° interior angle)
- N=4: Square (90° interior angle)
- N=5: Pentagon (108° interior angle)
- N=6: Hexagon (120° interior angle)
Extended polygons
- N=8: Octagon (135° interior angle)
- N=10: Decagon (144° interior angle)
- N=12: Dodecagon (150° interior angle)
- N→∞: Circle (180° limit angle)
Applications of the N-gon calculator
The universal N-gon calculator finds versatile applications:
Technical design
- CAD programs and technical drawings
- Mechanical engineering components
- Architectural floor plans
- Precision tools
Education & research
- Mathematics education and geometry
- Engineering sciences
- Crystallography and materials science
- Computer graphics and animation
Industry & production
- Manufacturing and punching technology
- Optical systems and prisms
- Packaging industry
- Jewelry and watch manufacturing
Creativity & games
- Game development and level design
- Puzzles and brain games
- Art projects and installations
- 3D printing and prototyping
Universal formulas for regular N-gons
Area A
Universal area formula for all N
Perimeter P
Simple: N times the side length
Circumradius rₐ
Radius of the circumcircle
Inradius rᵢ
Apothem (radius of the incircle)
Interior angle α
Each interior angle of the N-gon
Central angle β
Angle between two radii
Radius ratio
Circumradius to inradius ratio
Circle approximation
For large N, the polygon approaches a circle
Calculation example for an N-gon
Given
Find: All properties of the regular hexagon
1. Calculate basic measures
Perimeter and area
2. Radii and angles
Circumradius, inradius and interior angle
3. Universal formulas in action
All values result from the universal N-gon formulas
4. Complete N-gon analysis
The universal N-gon calculator works for all regular polygons!
The universal N-gon calculator: Geometry unified
The universal N-gon calculator is the most powerful tool in polygon geometry. With a single set of formulas, all regular polygons from N=3 to N→∞ can be calculated. It unites the entire diversity of regular polygons in elegant mathematical expressions.
The power of universal formulas
The mathematical beauty lies in the universality of trigonometry:
- One parameter N determines everything: All properties derive from the number of vertices
- Trigonometric elegance: sin(π/N), cos(π/N), tan(π/N) as basis
- Continuous transition: From N=3 (triangle) to N→∞ (circle)
- Scale invariance: Formulas work for any size
- Construction theory: Connection to Gaussian constructibility
From finite to infinite: The transition to the circle
The N-gon calculator shows the fascinating transition from polygons to circles:
Convergence behavior
With increasing N, all polygon properties approach those of the circle. Already at N=20, the difference is visually barely noticeable.
Archimedes' method
Archimedes already used this idea in 250 BC for π approximation: He calculated N-gons with N=96 for precise π values.
Modern applications
In computer graphics, circles are approximated by N-gons with high N. The universal formulas enable efficient calculations.
Limit values
lim(N→∞) sin(π/N)/(π/N) = 1 and similar limits show the deep connection between geometry and analysis.
Practical applications in science and technology
The universal N-gon calculator finds wide practical application:
- CAD software: Automatic polygon generation for technical drawings
- Crystallography: Analysis of N-fold symmetric crystal structures
- Optics: Calculation of prisms and optical elements
- Mechanical engineering: Gears, couplings and rotationally symmetric parts
- Architecture: Floor plans with special symmetries
- Packaging technology: Optimal space utilization with polygonal cross-sections
Education and research
As a universal tool, the N-gon calculator serves various educational goals:
Mathematical education
Students can experimentally discover how polygon properties change with N. Trigonometry becomes tangible and clear.
Engineering education
Future engineers learn to work with parametric geometry systems and their practical application.
Research
In materials science, N-gon calculations help understand quasicrystals and complex symmetries.
Computational Geometry
Algorithms for polygon processing are based on universal N-gon formulas for efficiency and accuracy.
Summary
The universal N-gon calculator is more than just a calculation tool - it is a window into the fundamental unity of geometry. It shows how all regular polygons follow a common mathematical logic and how discrete shapes continuously evolve into circles. From practical application in engineering and design to theoretical exploration of geometric principles, it unites simplicity with power. It demonstrates that behind the apparent diversity of the polygon world stand elegant, universal laws that describe both the equilateral triangle and the approximately circular 1000-gon. In a world increasingly shaped by parametric geometry and algorithmic design, the universal N-gon calculator remains a fundamental and indispensable tool.
|
|