Concave Hexagon Calculator
Calculator and formulas for concave hexagons
Concave Hexagon Calculator
Concave Hexagon
A concave hexagon is equilateral but not regular. At least one interior angle > 180° makes it concave.
Concave Hexagon
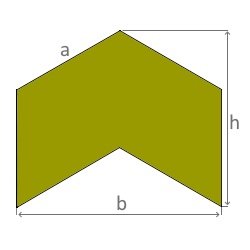
The diagram shows an equilateral concave hexagon.
All 6 sides are equal, but the angles are different.
What is a Concave Hexagon?
A concave hexagon is fundamentally different from a regular hexagon:
- Equilateral: All 6 sides are of equal length
- Not Regular: The angles are not equal
- Concavity: At least one interior angle is > 180°
- Bent Inward: The shape "caves in" on itself
- Star-like Silhouette: A characteristic shape
- Special Geometry: Unique properties
Geometric Properties
The concave hexagon exhibits fascinating geometric properties:
Angle Properties
- Sum of Angles: (6-2) × 180° = 720°
- At least one angle > 180° (concave)
- Other angles can be < 180°
- Unequal angle distribution
Dimensional Relationships
- All sides: a (equilateral)
- Width: b = √3 · a
- Height: h = 1.5 · a
- Compact, star-like shape
Mathematical Relationships
The concave hexagon follows specific mathematical laws:
Area Calculation
The area is equivalent to 2/3 of the area of a regular hexagon with the same side length.
Proportions
The ratio of width to height is constant and derives from the geometric construction.
Applications of Concave Hexagons
Concave hexagons find specialized applications in:
Design & Art
- Modern logo design
- Architectural accents
- Decorative art objects
- Graphic patterns and ornaments
Technical Applications
- Special tools and wrenches
- Mechanical engineering components
- Optical apertures (special shape)
- Puzzle and game components
Game Design
- Strategy games with special tiles
- Puzzle components
- Decorative game board elements
- 3D printing models
Science
- Geometric studies
- Mathematical modeling
- Computer graphics algorithms
- Topological investigations
Formulas for the Concave Hexagon
Area A
A remarkably simple formula involving √3
Perimeter P
Same as for a regular hexagon
Width b
Horizontal extent
Height h
Vertical extent
Side length a (from Area)
Backward calculation
Relation to Regular Hexagon
An interesting geometric relationship
Example Calculation for a Concave Hexagon
Given
Required: All properties of the concave hexagon
1. Calculate Basic Measures
Perimeter and Area
2. Calculate Dimensions
Width and Height
3. Comparison with Regular Hexagon
The concave hexagon is more space-efficient
4. Complete Summary
Characteristic: Star-like, inward-curving shape
The Concave Hexagon: A Geometric Peculiarity
The concave hexagon is a fascinating geometric shape that demonstrates how varying angles while keeping side lengths equal can result in entirely new properties. It serves as an example of the diversity of geometric possibilities beyond regular shapes.
Definition and Basic Properties
A concave polygon is characterized by having at least one interior angle greater than 180°:
- Concavity: At least one interior angle > 180° (reflex angle)
- Equilateral: All six sides have the same length
- Non-Regularity: The angles are not all equal
- Star Shape: The shape "caves inward"
- Simply Connected: Despite concavity, it remains simply connected
Mathematical Analysis of its Special Geometry
The concave hexagon exhibits interesting mathematical relationships:
Area Ratios
The area is exactly √3 · a², which is 2/3 of the area of a regular hexagon. This elegant relationship arises from the specific angle distribution.
Proportionality
The ratio of width to height (√3 : 1.5) is constant and independent of size, which is characteristic of this geometric shape.
Symmetry Properties
Although not regular, the concave hexagon possesses special symmetries. It has a vertical axis of reflection and exhibits 2-fold rotational symmetry.
Constructive Aspects
It is constructed by selectively "bending inward" two opposite sections of a regular hexagon while maintaining the side lengths.
Applications in Design and Technology
Despite its specialization, the concave hexagon finds practical applications:
- Industrial Design: Special tools with unusual grip shapes
- Architecture: Decorative elements with a unique aesthetic
- Art and Graphics: Logos and symbols with an "inward-caving" characteristic
- Game Design: Puzzle pieces and game components with high recognition value
- 3D Printing: Objects that are both compact and visually interesting
Geometric Relationships and Variations
The concave hexagon is related to other geometric shapes:
Regular Hexagon
The regular hexagon can be considered a "limiting case" where all angles are 120°. The concave hexagon is formed by increasing certain angles beyond 180°.
Stars and Star Polygons
It is related to star shapes, but without self-intersection. It can be interpreted as an "inward-pointing star".
Other Concave Polygons
As a member of the concave polygon class, it exhibits characteristic properties like reduced area for the same side lengths.
Topological Properties
Despite its concavity, it remains simply connected and shows how local changes in shape can affect global properties.
Summary
The concave hexagon demonstrates the diversity of geometric shapes beyond the well-known regular polygons. Its elegant mathematical relationships — especially the √3 factors and the 2/3 area ratio — show how geometric variation leads to new, yet harmonious proportions. It serves as an example that even unusual shapes are mathematically describable and can find practical applications. In a world increasingly seeking unique design solutions, the concave hexagon offers an interesting alternative to conventional forms.
|
|