Unregelmäßiges Achteck berechnen
Rechner und Formeln für das verlängerte Oktagon
Unregelmäßiges Achteck Rechner
Das unregelmäßige Achteck
Ein unregelmäßiges Achteck ist ein verlängertes Oktagon mit zwei verschiedenen Seitenlängen aber gleichen Innenwinkeln von 135°.
Achteck-Struktur
Das unregelmäßige Achteck hat zwei verschiedene Seitenlängen.
Alle Innenwinkel betragen einheitlich 135°.
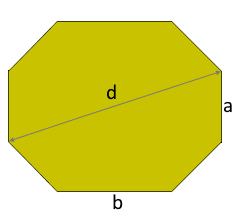
Das unregelmäßige verlängerte Achteck
Das unregelmäßige Achteck ist eine spezielle Form des Oktagons mit einzigartigen Eigenschaften:
- Acht Seiten: 6 Seiten der Länge a, 2 Seiten der Länge b
- Gleiche Winkel: Alle Innenwinkel betragen 135°
- Verlängerte Form: Rechteckiger Mittelteil mit abgeschrägten Ecken
- Einfache Berechnung: Nur zwei Parameter erforderlich
- Praktische Form: Häufig in technischen Anwendungen
- √2-Beziehungen: Mathematisch elegante Proportionen
Winkel-Eigenschaften
Die Winkel-Struktur des unregelmäßigen Achtecks ist bemerkenswert einheitlich:
Innenwinkel
- Alle 8 Innenwinkel = 135°
- Summe: 8 × 135° = 1080°
- Entspricht der Oktagon-Formel: (8-2) × 180°
- 45° mehr als rechter Winkel
Außenwinkel
- Alle 8 Außenwinkel = 45°
- Summe: 8 × 45° = 360°
- Entspricht der allgemeinen Regel für Polygone
- Halber rechter Winkel pro Ecke
Geometrische Struktur-Analyse
Die geometrische Struktur des verlängerten Achtecks:
Aufbau-Prinzip
- Mittelteil: Rechteck der Größe (b-a) × h
- Seitenteile: 2 Quadrate der Größe a × a
- Ecken: 4 abgeschrägte 45°-Dreiecke
- Symmetrie: Horizontal und vertikal symmetrisch
√2-Mathematik
- Höhe: h = a(1 + √2)
- Länge: l = a(1 + √2) + b - a
- √2 ≈ 1.414: Fundamental für 45°-Geometrie
- Elegante Formeln: Minimale Komplexität
Anwendungen des unregelmäßigen Achtecks
Das verlängerte Achteck findet vielfältige praktische Anwendungen:
Maschinenbau & Technik
- Spezielle Werkzeugprofile
- Rohrleitungs-Querschnitte
- Getriebe- und Nockenformen
- Strukturelle Hohlprofile
Architektur & Bauwesen
- Fenster- und Türöffnungen
- Säulen- und Pfeilerprofile
- Dekorative Wandelemente
- Pavillon- und Gazebo-Grundrisse
Design & Kunst
- Möbeldesign und Tischplatten
- Logo-Gestaltung und Symbole
- Schmuck und dekorative Objekte
- Textilmuster und Ornamente
Verkehr & Infrastruktur
- Straßenschilder und Verkehrszeichen
- Tunnel- und Brückenprofile
- Parkplatz- und Flächenmarkierungen
- Leitplanken und Absperrungen
Formeln für das unregelmäßige Achteck
Länge l
Gesamtlänge des verlängerten Achtecks
Höhe h
Höhe basiert nur auf der kurzen Seite a
Umfang U
6 kurze Seiten plus 2 lange Seiten
Diagonale d
Pythagoras angewendet auf Länge und Höhe
Flächeninhalt A
Zusammengesetzt aus Quadraten, Dreiecken und Rechteck
√2-Konstante
Fundamental für 45°-Winkel-Geometrie
Innenwinkel
Alle Innenwinkel sind gleich groß
Rechenbeispiel für ein unregelmäßiges Achteck
Gegeben
Gesucht: Alle geometrischen Eigenschaften des verlängerten Achtecks
1. Grundmaße berechnen
Höhe und Gesamtlänge
2. Umfang und Diagonale
Gesamtumfang und Hauptdiagonale
3. Flächenberechnung
Zusammensetzung aus verschiedenen geometrischen Elementen
4. Vollständiges unregelmäßiges Achteck
Das vollständige verlängerte Achteck - praktische Form mit eleganter Mathematik
Das unregelmäßige Achteck: Praktische Geometrie
Das unregelmäßige verlängerte Achteck ist ein faszinierendes Beispiel dafür, wie praktische Anforderungen zu eleganten geometrischen Lösungen führen können. Als Oktagon mit zwei verschiedenen Seitenlängen, aber einheitlichen Innenwinkeln, verbindet es die Einfachheit regelmäßiger Formen mit der Flexibilität irregulärer Konstruktionen und findet dadurch breite Anwendung in Technik und Design.
Geometrische Eleganz trotz Irregularität
Die Besonderheit des verlängerten Achtecks liegt in seiner strukturellen Klarheit:
- Einheitliche Winkel: Alle 8 Innenwinkel betragen exakt 135°
- Zwei Seitenlängen: 6 kurze Seiten (a) und 2 lange Seiten (b)
- √2-Mathematik: Alle Beziehungen basieren auf √2 ≈ 1.414
- Modularer Aufbau: Rechteckiger Mittelteil mit abgeschrägten Enden
- Symmetrische Struktur: Horizontal und vertikal spiegelsymmetrisch
- Einfache Formeln: Trotz Irregularität mathematisch handhabel
Der 135°-Winkel: Geometrische Perfektion
Der einheitliche Innenwinkel von 135° macht dieses Oktagon besonders:
Mathematische Bedeutung
135° = 90° + 45°, die perfekte Kombination aus rechtem Winkel und 45°-Abschrägung. Dies ermöglicht sowohl orthogonale als auch diagonale Konstruktionselemente.
Konstruktive Vorteile
Der 135°-Winkel erlaubt saubere Übergänge zwischen horizontalen/vertikalen und diagonalen Elementen, ideal für Fertigungs- und Montageprozesse.
Ästhetische Harmonie
Die 45°-Abschrägungen (Außenwinkel) schaffen visuelle Dynamik, während die einheitlichen Winkel für Ruhe und Ordnung sorgen.
Praktische Anwendung
Standard-Werkzeuge und -Maschinen können 45°-Schnitte einfach ausführen, was die Herstellung vereinfacht und Kosten reduziert.
Vielseitige praktische Anwendungen
Das verlängerte Achteck findet Anwendung in vielen Bereichen:
- Maschinenbau: Profile für Wellen, Rohre und strukturelle Komponenten
- Architektur: Säulen, Pfeiler und dekorative Elemente
- Verkehrstechnik: Schilder, Markierungen und Leitplanken-Profile
- Möbeldesign: Tischplatten, Rahmen und funktionale Elemente
- Elektronik: Gehäuse und Kühlkörper-Profile
- Optik: Linsen- und Prismenformen für spezielle Anwendungen
Mathematische Betrachtungen und Optimierung
Die mathematische Struktur ermöglicht interessante Optimierungsansätze:
Flächenoptimierung
Bei gegebenem Umfang kann das Verhältnis a:b so gewählt werden, dass die Fläche maximiert oder für spezielle Anforderungen optimiert wird.
Materialeffizienz
Die einfachen Formeln erlauben präzise Materialbedarfsberechnung und Verschnittoptimierung in der industriellen Fertigung.
Strukturanalyse
Die einheitlichen Winkel vereinfachen die Spannungsanalyse und ermöglichen präzise Vorhersagen über Belastbarkeit und Verformung.
Fertigungsaspekte
Die Reduzierung auf nur zwei Parameter (a und b) vereinfacht Konstruktion, Fertigung und Qualitätskontrolle erheblich.
Zusammenfassung
Das unregelmäßige verlängerte Achteck zeigt exemplarisch, wie mathematische Eleganz und praktische Anwendbarkeit Hand in Hand gehen können. Seine scheinbare Irregularität verbirgt eine tiefe geometrische Ordnung: Die einheitlichen 135°-Winkel schaffen strukturelle Klarheit, während die zwei verschiedenen Seitenlängen die nötige Flexibilität für vielfältige Anwendungen bieten. Von der √2-basierten Mathematik bis zur industriellen Fertigung demonstriert diese Form, dass wahre geometrische Schönheit nicht in perfekter Regelmäßigkeit liegt, sondern in der intelligenten Balance zwischen Ordnung und Anpassungsfähigkeit. In einer Welt, die sowohl Effizienz als auch Vielseitigkeit fordert, bietet das verlängerte Achteck eine optimale Lösung - mathematisch durchdacht, technisch umsetzbar und ästhetisch ansprechend.
|
|