Fehlerfunktion erf(x) berechnen

Online Rechner und Formel zur Berechnung der Fehlerfunktion erf(x)

erf(x) Rechner

Fehlerfunktion

Der Rechner berechnet die Fehlerfunktion erf(x), eine wichtige spezielle Funktion in der Mathematik und Statistik.

Reelle Zahl als Argument für die Fehlerfunktion
Resultat
erf(x):

Fehlerfunktion Kurve


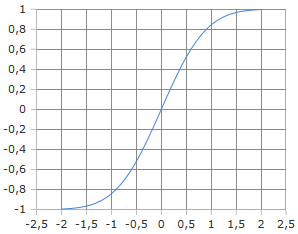
Erf Funktion

Grafische Darstellung der Fehlerfunktion erf(x) mit charakteristischem S-förmigen Verlauf.

Formeln zur erf(x) Funktion

Fehlerfunktion
\[\displaystyle erf(x)= \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2}dt\]
Komplementäre Fehlerfunktion
\[\displaystyle erfc(x)= \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2}dt\]
Beziehung
\[\displaystyle erf(x)+erfc(x)=1\]

Beschreibung der Fehlerfunktion

Mathematische Definition

Der Rechner auf dieser Seite berechnet die Fehlerfunktion erf(x). Die Fehlerfunktion ist eine spezielle mathematische Funktion, die in der Wahrscheinlichkeitstheorie und Statistik eine wichtige Rolle spielt.

Hinweise zur Berechnung

Zur Berechnung geben Sie das Argument x ein. Dann klicken Sie den Button 'Rechnen'.

Eigenschaften und Anwendungen

Normalverteilung

Die Fehlerfunktion ist eng mit der kumulativen Verteilungsfunktion der Normalverteilung verknüpft.

Eigenschaften
  • erf(0) = 0
  • erf(∞) = 1
  • erf(-x) = -erf(x) (ungerade Funktion)
Anwendungsbereiche

Statistik, Wahrscheinlichkeitstheorie, Physik, Ingenieurswissenschaften und Signalverarbeitung.


Wahrscheinlichkeiten

Geburtstagsparadoxon • Satz von Bayes • Zentraler Grenzwertsatz

Statistik Funktionen

Arithmetisches Mittel (Durchschnitt) • Empirische Inverse Verteilungsfunktion • Empirische Verteilungsfunktion • Five-Number Summary • Empirische inverse Verteilungsfunktion CDF • Geometrisches Mittel • Gepoolte Standardabweichung • Gepoolte Varianz • Harmonisches Mittel • Kontraharmonisches Mittel • Kovarianz • Kurtosis (Wölbung) • Log-Geometrisches Mittel • Median • Modus • Oberes Quartil • Skewness (Statistische Schiefe) • Standardabweichung • Unteres Quartil • Varianz

Statistik Distanz Funktionen

Dice Index • Hellingerabstand • Jaccard Index • Mittlerer Absoluter Fehler • Mittlerer Quadratischer Fehler • Summe der Absoluten Differenz • Summe der Abweichungsquadrate

Kombinatorik Funktionen

Kombinationen ohne Wiederholung • Kombinationen mit Wiederholung • Permutationen ohne Wiederholung • Produktregel • Variationen ohne Wiederholung • Variationen mit Wiederholung • Aktivitäten Auswahl Problem