Inverse komplementäre Fehlerfunktion erfci(x) berechnen

Rechner und Formel zur Berechnung der inversen komplementären Fehlerfunktion erfci(x)

erfci(x) Rechner

Inverse komplementäre Fehlerfunktion

Der Rechner berechnet die inverse komplementäre Fehlerfunktion erfci(x), die Umkehrfunktion von erfc(x) mit der Eigenschaft erfci(erfc(y)) = y.

Wert zwischen 0 und 2 für die inverse komplementäre Fehlerfunktion
Resultat
erfci(x):

Inverse komplementäre Fehlerfunktion Kurve


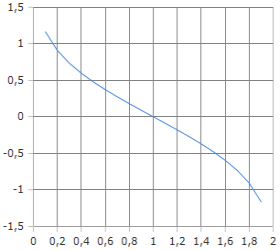
Erfci Funktion

Grafische Darstellung der inversen komplementären Fehlerfunktion erfci(x) mit charakteristischem monoton steigenden Verlauf.

Formeln zur erfci(x) Funktion

Inverse komplementäre Fehlerfunktion
\[\displaystyle erfci(x) = erfc^{-1}(x)\]
Inverse Eigenschaft
\[\displaystyle erfc^{-1}(erfc(x)) = x\]
Definitionsbereich
\[0 < x < 2\]
Komplementäre Fehlerfunktion
\[\displaystyle erfc(x)= \frac{2}{\sqrt{\pi}} \int_x^{\infty} e^{-t^2}dt\]
Beziehung
\[\displaystyle erf(x)+erfc(x)=1\]

Beschreibung der inversen komplementären Fehlerfunktion

Mathematische Definition

Der Rechner auf dieser Seite berechnet die inverse komplementäre Fehlerfunktion erfci(x). Diese Funktion ist die Umkehrfunktion der komplementären Fehlerfunktion erfc(x) und wird zur Bestimmung von Quantilen in der Statistik verwendet.

Hinweise zur Berechnung

Zur Berechnung geben Sie das Argument x ein. Dann klicken Sie den Button 'Rechnen'. Das Argument muss im Bereich 0 < x < 2 liegen.

Eigenschaften und Anwendungen

Umkehrfunktion

Die inverse komplementäre Fehlerfunktion ist die Umkehrfunktion von erfc(x): erfci(erfc(y)) = y

Definitionsbereich
  • Eingabe: 0 < x < 2
  • erfci(1) = 0
  • erfci(0) = +∞
  • erfci(2) = -∞
Anwendungsbereiche

Quantilberechnung in der Statistik, Monte-Carlo-Simulationen, Zufallszahlengenerierung und inverse Transformation in der Wahrscheinlichkeitstheorie.


Wahrscheinlichkeiten

Geburtstagsparadoxon • Satz von Bayes • Zentraler Grenzwertsatz

Statistik Funktionen

Arithmetisches Mittel (Durchschnitt) • Empirische Inverse Verteilungsfunktion • Empirische Verteilungsfunktion • Five-Number Summary • Empirische inverse Verteilungsfunktion CDF • Geometrisches Mittel • Gepoolte Standardabweichung • Gepoolte Varianz • Harmonisches Mittel • Kontraharmonisches Mittel • Kovarianz • Kurtosis (Wölbung) • Log-Geometrisches Mittel • Median • Modus • Oberes Quartil • Skewness (Statistische Schiefe) • Standardabweichung • Unteres Quartil • Varianz

Statistik Distanz Funktionen

Dice Index • Hellingerabstand • Jaccard Index • Mittlerer Absoluter Fehler • Mittlerer Quadratischer Fehler • Summe der Absoluten Differenz • Summe der Abweichungsquadrate

Kombinatorik Funktionen

Kombinationen ohne Wiederholung • Kombinationen mit Wiederholung • Permutationen ohne Wiederholung • Produktregel • Variationen ohne Wiederholung • Variationen mit Wiederholung • Aktivitäten Auswahl Problem