RC Integrator berechnen
Rechner und Formeln zur Berechnung eines RC Integrierglieds
Integrierer berechnen
RC Integrierglied
Mit dieser Funktion können die Eigenschaften eines RC Integrierglieds berechnet werden. Die Funktion berechnet den Kondensator, den Widerstand oder die Periodendauer bzw. die Frequenz.
Integrierglied
Impulsformerstufe
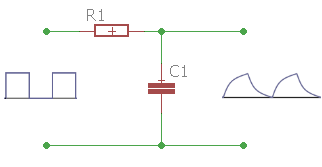
Das Integrierglied funktioniert als Impulsformerstufe. Das RC-Glied erzeugt aus einer Rechteckspannung am Eingang eine rampenförmige am Ausgang der Schaltung.
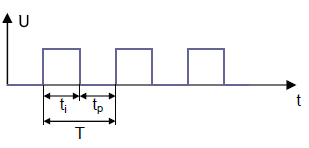
Zeitkonstante τ (tau)
Die Zeitkonstante eines RC-Glied ist das Produkt von R · C. Die Maßeinheit ist die Sekunde. Das Formelzeichen ist der griechische Buchstabe τ (tau).
Nach 5τ liegt die Ladung bei ca. 99,3%.
RC Integrierglied - Theorie und Formeln
Funktionsweise des Integrierglieds
Das Integrierglied funktioniert als Impulsformerstufe. Das RC-Glied erzeugt aus einer Rechteckspannung am Eingang eine rampenförmige Spannung am Ausgang der Schaltung. Die Integration erfolgt durch die langsame Aufladung des Kondensators.
Impulsformen bei verschiedenen Zeitkonstanten
t1 = 5τ Optimale Integration
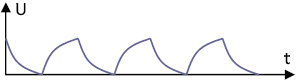
Wenn die Länge des Rechteckimpuls (t1) dem 5-fachen der Zeitkonstanten τ entspricht, entsteht eine optimale Rampenform.
t1 > 5τ Steilere Rampen
Wenn die Impulsdauer der Eingangsspannung größer als 5τ ist, werden steilere Rampenformen erzeugt.
Zeitkonstante und Ladeverhalten
Die Zeitkonstante τ (tau)
- Die Zeitkonstante ist das Produkt von R × C
- Maßeinheit: Sekunden (s)
- Formelzeichen: τ (griechischer Buchstabe tau)
- Nach 5τ liegt die Ladung bei ca. 99,3%
- Bestimmt die Geschwindigkeit der Rampenbildung
- Für gute Integration: t1 ≥ 5τ
Praktische Anwendungen
Signalverarbeitung:
Messtechnik:
Regelungstechnik:
Designrichtlinien
Optimale Dimensionierung
- Für gute Integration: t1 ≥ 5τ
- Für lineare Rampen: t1 ≥ 10τ
- Ausgangsamplitude: Abhängig von der Zeitkonstante
- Rampensteigung: Proportional zu 1/τ
- Belastung: Hoher Eingangswiderstand der folgenden Stufe
- Frequenzbereich: Abhängig von τ und gewünschter Genauigkeit
Mathematische Beziehungen
Grundformeln
Wobei n der Faktor ist (typisch 5 oder größer)
Umrechnungen
Berechnung der Komponenten bei gegebenem t1
Integrator vs. Differenziator
Unterschiede
Integrator (RC):
- Ausgang am Kondensator
- Erzeugt Rampen aus Rechtecken
- Langsame Änderungen
- Tiefpass-Charakter
Differenziator (CR):
- Ausgang am Widerstand
- Erzeugt Spikes aus Rechtecken
- Schnelle Änderungen
- Hochpass-Charakter
|
|