R/C zur gegebenen Ladespannung
Berechnung von R oder C zu einer gegebenen Ladespannung zu einem Zeitpunkt
R/C zur Ladespannung berechnen
RC Ladungsvorgang
Auf dieser Seite können Sie die Werte eines Kondensators oder Widerstands berechnen die erforderlich sind um an einem Kondensator eine bestimmte Ladespannung zu einem gegebenen Zeitpunkt zu erreichen.
RC Ladungsvorgang
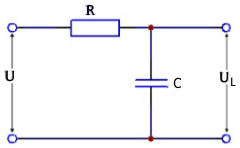
Legende
Berechnungsformeln
Ladungsvorgang
- Exponentialfunktion: UC(t) = U(1 - e-t/τ)
- Zeitkonstante: τ = RC
- 63% nach τ: Nach einer Zeitkonstante
- 99% nach 5τ: Praktisch vollständige Ladung
RC Ladungsvorgang - Theorie und Anwendungen
Der Kondensator-Ladevorgang
Beim Aufladen eines Kondensators über einen Widerstand folgt die Spannung am Kondensator einer Exponentialfunktion. Die Ladegeschwindigkeit wird durch die Zeitkonstante τ = RC bestimmt. Diese Berechnungen ermöglichen es, die erforderlichen Bauteilwerte für eine gewünschte Ladespannung zu einem bestimmten Zeitpunkt zu ermitteln.
Mathematische Grundlagen
Ladespannung über Zeit
Exponentialfunktion des Ladevorgangs mit τ = RC
Umstellung für R und C
Normalisierte Form zur Bauteilberechnung
Zeitkonstante und Ladeverhalten
Nach 1τ (63%)
Nach einer Zeitkonstante ist der Kondensator zu 63% geladen.
Nach 3τ (95%)
Nach drei Zeitkonstanten praktisch vollständig geladen.
Nach 5τ (99%)
Nach fünf Zeitkonstanten vollständige Ladung erreicht.
Praktische Anwendungen
Timing-Schaltungen:
Energieversorgung:
Signalverarbeitung:
Berechnungsbeispiele
Beispiel 1: Widerstand berechnen
Gegeben: C = 10µF, U = 12V, UC = 8V, t = 10ms
Ergebnis: Der erforderliche Widerstand beträgt etwa 918Ω.
Beispiel 2: Kondensator berechnen
Gegeben: R = 1kΩ, U = 5V, UC = 3V, t = 1ms
Ergebnis: Die erforderliche Kapazität beträgt etwa 1,1µF.
Design-Überlegungen
Wichtige Designaspekte
- Zeitkonstante: τ = RC bestimmt die Ladegeschwindigkeit
- Spannungsfestigkeit: Kondensator muss für Betriebsspannung ausgelegt sein
- Leckstrom: Reale Kondensatoren haben parasitäre Widerstände
- Toleranzen: Bauteilstreuungen beeinflussen das Zeitverhalten
- Temperatureinfluss: Kapazität und Widerstand sind temperaturabhängig
- ESR: Äquivalenter Serienwiderstand beeinflusst das Verhalten
Entladevorgang
Kondensator-Entladung
Bei der Entladung folgt die Spannung einer fallenden Exponentialfunktion. Nach einer Zeitkonstante sind noch 37% der Anfangsspannung vorhanden.
|
|