RC Serienschaltung berechnen
Rechner und Formeln zur Berechnung von Spannung und Leistung einer RC Serienschaltung
RC-Reihenschaltung Rechner
RC Serienschaltung
Diese Funktion berechnet die Spannungen, Leistungen, Strom, Schein- und Blindwiderstand einer Reihenschaltung aus einem Widerstand und einem Kondensator.
RC Serienschaltung
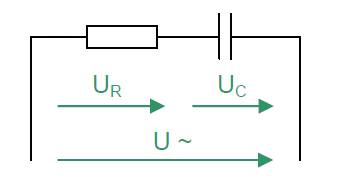
Serienschaltung Eigenschaften
- Gleicher Strom durch alle Bauteile
- Gesamtspannung ist Summe der Teilspannungen
- Impedanz größer als größter Einzelwiderstand
- Phasenverschiebung zwischen Spannungen
Grundformeln
Spannungs- und Widerstandsdreieck nach Pythagoras
Leistungsdreieck
- P: Wirkleistung (im Widerstand)
- Q: Blindleistung (im Kondensator)
- S: Scheinleistung (Gesamtleistung)
RC Serienschaltung - Theorie und Formeln
Grundlagen der RC Serienschaltung
Der Gesamtwiderstand der RC-Reihenschaltung im Wechselstromkreis wird als Scheinwiderstand oder Impedanz Z bezeichnet. Für die Gesamtschaltung gilt das Ohmsche Gesetz. Der Strom ist an jeder Messstelle gleich. Am Ohmschen Wirkwiderstand sind Strom und Spannung in Phase. Am kapazitiven Blindwiderstand des Kondensators eilt die Spannung dem Strom um −90° nach.
Spannungsdreieck
Spannungen
Widerstandsdreieck
Leistungen in der RC-Reihenschaltung
Die Multiplikation der Augenblickwerte von Spannung U und des Stroms I ergeben die Leistungskurve.
Wirkleistung
Die Wirkleistung wird im Widerstand in Wärme umgesetzt.
Blindleistung
Die Blindleistung pendelt zwischen dem Kondensator und dem Generator hin und her.
Scheinleistung
Die Scheinleistung ist eine rein rechnerische Größe.
Leistungsdreieck
Leistungszusammenhänge
Leistungsfaktor cos(φ)
Leistungsfaktor cos(φ)
Leistungsfaktor
Der Leistungsfaktor gibt an, wie viel der Scheinleistung S als Wirkleistung P umgesetzt wird. Je näher cos(φ) bei 1 liegt, desto effizienter ist die Energieübertragung.
Praktische Anwendungen
Filter-Schaltungen:
Timing-Schaltungen:
Kopplung:
Phasenverhalten
Phasenverschiebung
- Widerstand: Strom und Spannung in Phase (φ = 0°)
- Kondensator: Spannung eilt Strom um -90° nach
- Gesamtschaltung: Phasenwinkel zwischen 0° und -90°
- Kapazitiv: Bei XC > R wird die Schaltung kapazitiv
- Resistiv: Bei R > XC überwiegt der ohmsche Charakter
Frequenzabhängigkeit
Tiefe Frequenzen
- XC ist groß
- Impedanz wird von XC dominiert
- Große Phasenverschiebung
- Kondensator wirkt wie Sperre
Hohe Frequenzen
- XC ist klein
- Impedanz wird von R dominiert
- Kleine Phasenverschiebung
- Kondensator wirkt wie Kurzschluss
Design-Hinweise
Wichtige Designaspekte
- Spannungsaufteilung: Abhängig von Frequenz und Bauteilwerten
- Resonanz: Bei f = fg ist Z minimal
- Spannungsfestigkeit: Teilspannungen können größer als Gesamtspannung sein
- Verlustfaktor: Reale Kondensatoren haben zusätzlichen ESR
- Toleranzen: Bauteilstreuungen beeinflussen das Verhalten
- Temperatureinfluss: Kapazität und Widerstand sind temperaturabhängig
|
|