RC Parallelschaltung berechnen

Rechner und Formeln zur Berechnung von Strom und Leistung einer RC Parallelschaltung

RC Parallelschaltung

Der Rechner berechnet Strom, Leistungen, Schein- und Blindwiderstand in der Parallelschaltung eines Widerstands und eines Kondensators.

Kondensator C

Frequenz f

Widerstand R

Spannung U

Dezimalstellen

Ergebnisse

Blindwiderstand X_C:

Gesamtwiderstand Z:

Widerstandstrom I_R:

Kondensatorstrom I_C:

Gesamtstrom I:

Phasenwinkel φ:

Wirkleistung P:

Blindleistung Q:

Scheinleistung S:

Schaltbild

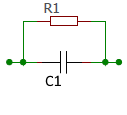
Parallelschaltung Eigenschaften

Gleiche Spannung an allen Bauteilen
Gesamtstrom ist Summe der Teilströme
Impedanz kleiner als kleinster Einzelwiderstand
Phasenverschiebung zwischen Teilströmen

Grundformeln

\[I=\sqrt{I_R^2+I_C^2}\] \[Z=\frac{X_C \cdot R}{\sqrt{R^2+X_C^2}}\]

Gesamtstrom und Impedanz der RC-Parallelschaltung.

Leistungen

Wirkleistung P: Nur im Widerstand
Blindleistung Q: Nur im Kondensator
Scheinleistung S: Geometrische Summe

RC Parallelschaltung - Theorie und Formeln

Grundlagen der RC-Parallelschaltung

Der Gesamtwiderstand der RC-Parallelschaltung im Wechselstromkreis wird als Scheinwiderstand oder Impedanz Z bezeichnet. Für die Gesamtschaltung gilt das Ohmsche Gesetz. Am Ohmschen Wirkwiderstand sind Strom und Spannung in Phase. Am kapazitiven Blindwiderstand des Kondensators eilt die Spannung dem Strom um −90° nach.

Formeln und Berechnungen

Stromdreieck

\[I=\sqrt{I_R^2+I_C^2}\]

I	Gesamtstrom
I_R	Strom durch Widerstand
I_C	Strom durch Kondensator

Leitwertdreieck

\[Y=\sqrt{G^2+B_C^2}\]

G	Wirkleitwert [1/R]
B_C	Blindleitwert [1/X_C]
Y	Scheinleitwert [1/Z]

Widerstandsdreieck

\[Z=\frac{X_C \cdot R}{\sqrt{R^2+X_C^2}}\]

X_C	Kapazitiver Blindwiderstand
R	Wirkwiderstand
Z	Impedanz

Leistungsberechnung

Wirkleistung

\[P=U \cdot I_R\]

Die Wirkleistung wird nur im Widerstand umgesetzt und in Wärme umgewandelt.

Blindleistung

\[Q=U \cdot I_C\]

Die Blindleistung pendelt zwischen Kondensator und Generator hin und her.

Scheinleistung

\[S=\sqrt{P^2+Q^2}\]

Die Scheinleistung ist eine rein rechnerische Größe.

Besonderheiten der Parallelschaltung

Wichtige Eigenschaften

Der Gesamtstrom ist die geometrische Summe der Teilströme
Die Spannung ist an allen Bauteilen gleich
Der Gesamtwiderstand ist kleiner als der kleinste Einzelwiderstand
Die Teilströme bilden ein rechtwinkliges Stromdreieck
Bei der Parallelschaltung arbeitet man mit Leitwerten
Die Phasenverschiebung zwischen Strom und Spannung ist frequenzabhängig

Praktische Anwendungen

Leistungsfaktor-Korrektur:

• Kompensation von Induktivitäten

• Verbesserung cos φ

• Reduzierung Blindstrom

• Energieeffizienz

Filter-Anwendungen:

• Hochpassfilter

• Frequenzweichen

• Audio-Technik

• Signalaufbereitung

Oszillatoren:

• RC-Oszillatoren

• Phasenschieber

• Frequenzgeneratoren

• Taktgeneratoren

Weitere Funktionen mit Kondensatoren

Serienschaltung mit Kondensatoren • Serienschaltung mit 2 Kondensatoren • Blindwiderstand eines Kondensators • Zeitkonstante eines R/C-Glieds • Ladespannung zu einem Zeitpunkt • Entladespannung zu einem Zeitpunkt • R oder C zu einer Ladespannung • RC Reihenschaltung berechnen • RC Parallelschaltung berechnen • RC Hochpass berechnen • RC Tiefpass berechnen • RC Differenzierglied berechnen • RC Integrierglied berechnen • RC Grenzfrequenz berechnen • R + C bei gegebener Impedanz