RC Tiefpass berechnen
Rechner und Formeln zur Berechnung der Parameter eines RC Tiefpasses
RC Tiefpass berechnen
RC Tiefpass Filter
Diese Funktion berechnet die Eigenschaften eines Tiefpasses aus Widerstand und Kondensator. Es wird bei der gegebenen Frequenz die Ausgangsspannung, Dämpfung und die Phasendrehung berechnet.
RC Tiefpass Schaltung
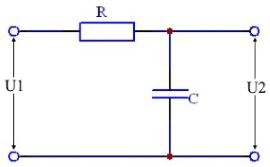
Symbol-Erklärungen
Tiefpass Eigenschaften
- Lässt tiefe Frequenzen durch
- Dämpft hohe Frequenzen
- -3dB bei Grenzfrequenz
- -20dB/Dekade Abfall
- Phasenverschiebung 0° bis -90°
Grenzfrequenz
Bei der Grenzfrequenz beträgt die Dämpfung -3dB.
RC Tiefpass - Theorie und Formeln
RC Tiefpass Grundlagen
Ein RC Tiefpass ist ein Filter erster Ordnung, der tiefe Frequenzen durchlässt und hohe Frequenzen dämpft. Der Ausgang wird am Kondensator abgenommen. Bei hohen Frequenzen hat der Kondensator einen niedrigen Widerstand, bei tiefen Frequenzen einen hohen.
Wichtige Formeln
Spannungsverhältnis
oder einfacher mit XC:
Blindwiderstand
Der kapazitive Blindwiderstand nimmt mit steigender Frequenz ab.
Dämpfung und Phase
Dämpfung in dB
oder direkt:
Phasenverschiebung
oder:
Grenzfrequenz und charakteristische Werte
Grenzfrequenz
Bei fg: Dämpfung = -3dB, Phase = -45°
Impedanz
Gesamtimpedanz der Schaltung
Zeitkonstante
Charakteristische Zeit der Schaltung
Frequenzverhalten
Frequenzgang Eigenschaften
- Tiefe Frequenzen (f ≪ fg): Keine Dämpfung, Phase → 0°
- Grenzfrequenz (f = fg): -3dB Dämpfung, Phase = -45°
- Hohe Frequenzen (f ≫ fg): Starke Dämpfung, Phase → -90°
- Flankensteilheit: -20dB/Dekade oberhalb fg
- Übertragungsfunktion: H(jω) = 1/(1 + jωRC)
Praktische Anwendungen
Audio-Filter:
Glättungsfilter:
Zeitglieder:
Design-Hinweise
Wichtige Designaspekte
- Grenzfrequenz-Wahl: Sollte deutlich über der höchsten zu übertragenden Frequenz liegen
- Kapazitätswahl: Größere C → niedrigere fg, aber größere Bauteile
- Widerstandswahl: Kompromiss zwischen Eingangsimpedanz und Signalpegel
- Belastungseffekte: Nachfolgende Stufe sollte hochohmig sein
- Toleranzen: Bauteilstreuungen beeinflussen die Grenzfrequenz
Mathematische Beziehungen
Grundformeln
Beziehung zwischen Zeitkonstante und Grenzfrequenz
Umrechnungen
Berechnung der Komponenten bei gegebener Grenzfrequenz
Tiefpass vs. Hochpass
Unterschiede
Tiefpass (RC):
- Ausgang am Kondensator
- Dämpft hohe Frequenzen
- Phase: 0° bis -90°
- Glättungscharakter
Hochpass (CR):
- Ausgang am Widerstand
- Dämpft tiefe Frequenzen
- Phase: +90° bis 0°
- Differenziercharakter
|
|
Weitere Funktionen mit Kondensatoren
Serienschaltung mit Kondensatoren • Serienschaltung mit 2 Kondensatoren • Blindwiderstand eines Kondensators • Zeitkonstante eines R/C-Glieds • Ladespannung zu einem Zeitpunkt • Entladespannung zu einem Zeitpunkt • R oder C zu einer Ladespannung • RC Reihenschaltung berechnen • RC Parallelschaltung berechnen • RC Hochpass berechnen • RC Tiefpass berechnen • RC Differenzierglied berechnen • RC Integrierglied berechnen • RC Grenzfrequenz berechnen • R + C bei gegebener Impedanz
|
|