Regelmäßiges N-Eck berechnen
Universeller Rechner für alle regelmäßigen Polygone
N-Eck Rechner
Universeller Polygon-Rechner
Ein regelmäßiges N-Eck hat N gleich lange Seiten und N gleich große Winkel. Universelle Formeln für alle Polygone.
Regelmäßiges N-Eck
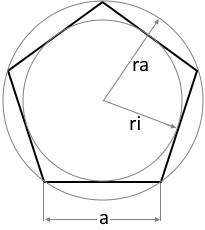
Das Diagramm zeigt ein Beispiel-Polygon mit Innen- und Außenkreis.
Alle N Seiten sind gleich lang, alle Innenwinkel sind gleich groß.
Der universelle N-Eck Rechner
Ein regelmäßiges N-Eck ist die allgemeinste Form eines regulären Polygons:
- N gleiche Seiten: Alle Seitenlängen sind identisch
- N gleiche Winkel: Jeder Innenwinkel = 180°(N-2)/N
- Winkelsumme: (N-2) × 180°
- Zentrumswinkel: 360°/N pro Segment
- N-fache Symmetrie: Rotations- und Spiegelsymmetrie
- Universelle Formeln: Funktionieren für alle N ≥ 3
Universelle Polygon-Formeln
Diese universellen Formeln funktionieren für alle regelmäßigen Polygone:
Grundformeln
- Umfang: P = N · a
- Fläche: A = (N/4) · cot(π/N) · a²
- Innenwinkel: α = 180°(N-2)/N
- Zentrumswinkel: β = 360°/N
Kreis-Beziehungen
- Außenradius: rₐ = a/(2·sin(π/N))
- Innenradius: rᵢ = a/(2·tan(π/N))
- Verhältnis: rₐ/rᵢ = 1/cos(π/N)
- Apothem = Innenradius
Bekannte Polygon-Beispiele
Übersicht der häufigsten regelmäßigen Polygone und ihrer Eigenschaften:
Grundpolygone
- N=3: Dreieck (60° Innenwinkel)
- N=4: Quadrat (90° Innenwinkel)
- N=5: Pentagon (108° Innenwinkel)
- N=6: Hexagon (120° Innenwinkel)
Erweiterte Polygone
- N=8: Oktagon (135° Innenwinkel)
- N=10: Dekagon (144° Innenwinkel)
- N=12: Zwölfeck (150° Innenwinkel)
- N→∞: Kreis (180° Grenzwinkel)
Anwendungen des N-Eck Rechners
Der universelle N-Eck Rechner findet vielseitige Anwendungen:
Technisches Design
- CAD-Programme und technische Zeichnungen
- Maschinenbau-Komponenten
- Architektonische Grundrisse
- Präzisionswerkzeuge
Bildung & Forschung
- Mathematikunterricht und Geometrie
- Ingenieurwissenschaften
- Kristallographie und Materialwissenschaft
- Computergrafik und Animation
Industrie & Produktion
- Fertigungstechnik und Stanztechnik
- Optische Systeme und Prismen
- Verpackungsindustrie
- Schmuck- und Uhrenherstellung
Kreativität & Spiele
- Spieleentwicklung und Level-Design
- Puzzle und Denkspiele
- Kunstprojekte und Installationen
- 3D-Druck und Prototyping
Universelle Formeln für regelmäßige N-Ecke
Flächeninhalt A
Universelle Flächenformel für alle N
Umfang P
Einfach: N-mal die Seitenlänge
Außenradius rₐ
Radius des Umkreises
Innenradius rᵢ
Apothem (Radius des Inkreises)
Innenwinkel α
Jeder Innenwinkel des N-Ecks
Zentrumswinkel β
Winkel zwischen zwei Radien
Radius-Verhältnis
Außen- zu Innenradius-Verhältnis
Kreis-Näherung
Für große N nähert sich das Polygon dem Kreis
Rechenbeispiel für ein N-Eck
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Sechsecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Radien und Winkel
Außenradius, Innenradius und Innenwinkel
3. Universelle Formeln in Aktion
Alle Werte ergeben sich aus den universellen N-Eck Formeln
4. Vollständige N-Eck Analyse
Der universelle N-Eck Rechner funktioniert für alle regulären Polygone!
Der universelle N-Eck Rechner: Geometrie vereint
Der universelle N-Eck Rechner ist das mächtigste Werkzeug der Polygon-Geometrie. Mit einem einzigen Satz von Formeln können alle regelmäßigen Polygone von N=3 bis N→∞ berechnet werden. Er vereint die gesamte Vielfalt der regulären Vielecke in eleganten mathematischen Ausdrücken.
Die Macht der universellen Formeln
Die mathematische Schönheit liegt in der Universalität der Trigonometrie:
- Ein Parameter N bestimmt alles: Alle Eigenschaften ergeben sich aus der Eckenzahl
- Trigonometrische Eleganz: sin(π/N), cos(π/N), tan(π/N) als Basis
- Kontinuierlicher Übergang: Von N=3 (Dreieck) bis N→∞ (Kreis)
- Skalierungs-Invarianz: Formeln funktionieren für jede Größe
- Konstruktions-Theorie: Verbindung zu Gauß'scher Konstruierbarkeit
Von endlich zu unendlich: Der Grenzübergang zum Kreis
Der N-Eck Rechner zeigt den faszinierenden Übergang von Polygonen zum Kreis:
Konvergenz-Verhalten
Mit steigendem N nähern sich alle Polygon-Eigenschaften denen des Kreises. Bereits bei N=20 ist der Unterschied visuell kaum erkennbar.
Archimedes'sche Methode
Archimedes nutzte bereits 250 v.Chr. diese Idee zur π-Approximation: Er berechnete N-Ecke mit N=96 für präzise π-Werte.
Moderne Anwendungen
In Computergrafik werden Kreise durch N-Ecke mit hohem N approximiert. Die universellen Formeln ermöglichen effiziente Berechnungen.
Grenzwerte
lim(N→∞) sin(π/N)/(π/N) = 1 und ähnliche Grenzwerte zeigen die tiefe Verbindung zwischen Geometrie und Analysis.
Praktische Anwendungen in Wissenschaft und Technik
Der universelle N-Eck Rechner findet breite praktische Anwendung:
- CAD-Software: Automatische Polygon-Generierung für technische Zeichnungen
- Kristallographie: Analyse von N-fach symmetrischen Kristallstrukturen
- Optik: Berechnung von Prismen und optischen Elementen
- Maschinenbau: Zahnräder, Kupplungen und rotationssymmetrische Teile
- Architektur: Grundrisse mit speziellen Symmetrien
- Verpackungstechnik: Optimale Raumausnutzung bei polygonalen Querschnitten
Bildung und Forschung
Als universelles Werkzeug dient der N-Eck Rechner verschiedenen Bildungszielen:
Mathematische Bildung
Schüler können experimentell entdecken, wie sich Polygon-Eigenschaften mit N verändern. Trigonometrie wird greifbar und anschaulich.
Ingenieurausbildung
Angehende Ingenieure lernen den Umgang mit parametrischen Geometrie-Systemen und deren praktischer Anwendung.
Forschung
In der Materialwissenschaft helfen N-Eck Berechnungen beim Verständnis von Quasikristallen und komplexen Symmetrien.
Computational Geometry
Algorithmen zur Polygon-Bearbeitung basieren auf den universellen N-Eck Formeln für Effizienz und Genauigkeit.
Zusammenfassung
Der universelle N-Eck Rechner ist mehr als nur ein Berechnungswerkzeug - er ist ein Fenster in die fundamentale Einheit der Geometrie. Er zeigt, wie alle regelmäßigen Polygone einer gemeinsamen mathematischen Logik folgen und wie sich diskrete Formen kontinuierlich zum Kreis entwickeln. Von der praktischen Anwendung in Technik und Design bis zur theoretischen Erforschung geometrischer Prinzipien vereint er Einfachheit mit Mächtigkeit. Er demonstriert, dass hinter der scheinbaren Vielfalt der Polygonwelt elegante, universelle Gesetze stehen, die sowohl das gleichseitige Dreieck als auch das annähernd kreisförmige 1000-Eck beschreiben. In einer Welt, die zunehmend von parametrischer Geometrie und algorithmischem Design geprägt ist, bleibt der universelle N-Eck Rechner ein fundamentales und unverzichtbares Werkzeug.
|
|